Review - Electric Fields

*Check the Electric Fields Outline  for recommended problems to try.

1.

(a) Find the magnitude and direction of the force of +Q on q_o at (i) P₁ and (ii) P₂ in Fig 1a below. (b) Find the magnitude and direction of the force of -Q on q_o at (i) P₁ and (ii) P₂ in Fig.1b below. Take Q = 2 x 10^-6 C and q_o = 10^-12 C.

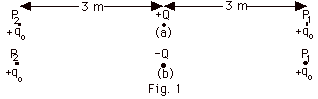
2.

Now imagine that all the +q_o's are removed from Fig. 1 above.  Find the magnitude and the direction of the electric field (a) in Fig. 1a and (b) in Fig. 1b at P₁ and P_2.

3.

(a) Find the electric field at point P in Fig. 2 below. (b) Repeat for q₂ = +1 nC.

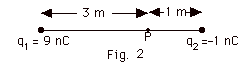
4.

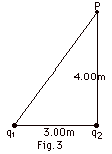
In Fig. 3 below,  q₁ = +1.00 µC and q₂ = -0.0800 µC.  Find the direction and magnitude of the electric field at point P.

5.

Find (a) the electric field, direction and magnitude, at P (4.00 m, 5.00m) in Fig. 4 below due to q₁ = +5.00 x 10^-6 C at (0, 2.00 m), q₂ = -3.00 x 10^-6 C at
(4.00 m, 0), and q₃ = +1.6 x 10^-6 C at (0, 5.00 m) and (b) the force on q₄ = +2.0 x 10^-6 C placed at P.

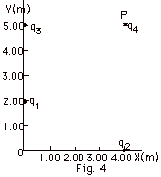
6.

Two positive point charges repel each other. Explain this experimental result in terms of the field of one charge acting on the other charge.

7.

A small positive charge is placed in the electric field of a fixed positive point charge. Is the acceleration of the small positive charge constant? Explain your answer.

8.

Two point charges, q₁ = +1.0 x 10^-6 C and q₂ = -4.0 x 10^-6 C, are separated by a distance of 0.10 m. First discuss two of three points in the figure below where the electric field cannot be zero and then find the point along the line passing through the two charges at which the electric field due to them is zero.

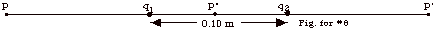
9.

(a) If a Gaussian surface has 15 field lines (the electric flux) leaving it when it surrounds a point charge of +10.0 µC and 75 field lines entering it when it surrounds an unknown point charge, what is the amount of charge on the unknown? (b) If a net number of electric field lines point out of a Gaussian surface, does that mean there are no negative charges in the interior?

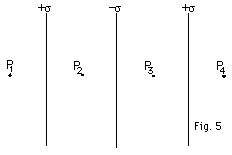
10.

Three infinite sheets of charge are parallel to each other, as is shown in Fig. 5 below. The sheet on the left has a uniform surface charge density +σ, the one in the middle a uniform surface charge density -σ and the one on the right a uniform surface charge density of +σ. Find the electric field at (a) P₁, (b) P₂,
(c) P₃, and (d) P₄.

11.

The number of electric field lines per unit area crossing a surface at a right angle to the surface equals the electric field at the surface. Show that the number of field lines emanating from a point charge +Q is 4 πkQ = Q/ ε_o. Hint: Surround the charge Q by a hypothetical spherical surface of radius r and find the product of the electric field due to Q and the surface area of the sphere.

12.

Charge Q is distributed uniformly throughout a sphere of radius R (Fig. 6 below). Find the electric field for (a) r ≤ R, (b) r ≥ R. (c) Sketch a graph of E as a function of r.

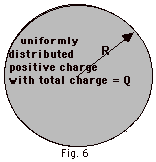
13.

A conducting sphere of charge +Q and radius a is concentric with a conducting, spherical shell that has a net charge of 0. The shell has inner radius b and outer radius c. (a) Where are the charges?

Find the electric field for (b) r ≤ a, (c) a ≤ r ≤ b, (d) b ≤ r ≤ c and (e) r ≥ c.

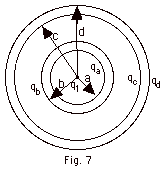
14.

A point charge q_i = 8.85 µC is at the center of two concentric conducting shells as shown in Fig. 7 below. The net charge on the inner shell is -17.70 µC and the net charge on the outer shell is +8.85 µC. Find (a) the inner charge q_a and the outer charge q_b on the inner shell and (b) the inner charge q_c and the outer charge q_d on the outer shell. (c) Sketch a graph of the net flux through a Gaussian sphere centered on the point charge as a function of the distance r from the point charge.

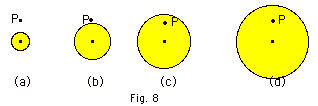
*15.

Figure 8 below represents four spheres of different radii R, but with the same total charge Q distributed uniformly through the spheres. Point P in the figures is the same distance from the center of each sphere. (a) Rank the spheres according to their volume charge density ρ, greatest first. (b) Rank the spheres according to the magnitude of the electric field they produce at point P, greatest first.

^*Taken from Halliday,/Resnick/ Walker, Fundamentals of Physics, Sixth Edition, Wiley

16.

Can two electric field lines intersect? Explain your answer.

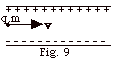
17.

A particle of mass m = 1.6 x 10^-27 kg and charge q = +3.2 x 10^-19 C , moving with a constant horizontal velocity v = 4.0 x 10⁶ m/s enters the constant electric field E = 20 x 10² N/C between the parallel plates of Fig. 9 below. Find (a) the magnitude and direction of the electric force on the particle due to E, (b) the acceleration due to the electric field, (c) the acceleration due to the gravitational force, (d) how long it takes for the particle to leave the plates if the length of the plates is 0.80 m and (e) how far it will be from halfway between the plates as it leaves the plates.

18.

A proton of charge +e and mass m is placed in an electric field E. Find (a) the acceleration of the proton and (b) the velocity and displacement of the proton in time t after entering the field. Assume the initial velocity of the proton is zero.

19.

An alpha particle has charge +2e and a mass that is four times the mass of a proton. If an alpha particle is placed in the same electric field as the proton in Problem 18, compare the acceleration, velocity and displacement of the alpha particle with that of the proton. Again assume that the initial velocity of the alpha particle is zero.

20.

Discuss the possible difference between the force on a charged particle in a constant electric field when its initial velocity is zero and when it has an initial velocity.

21.

An electron moves in a circular path around a long, uniformly charged wire carrying +2.5 nC/m. What is the speed of the electron?

22.

A small sphere with mass m carries charge q. It hangs from a silk thread that makes an angle Θ with a large, charged nonconducting sheet (Fig. 10 below). Find the sheet's surface charge density σ.

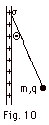
23.

Two identical dipoles are placed in a straight line as shown in Fig. 11a below. Find the direction of the electric force on each dipole in Fig. 11a.  Repeat for
Fig. 11b below.

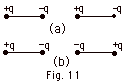
24.

An electric dipole consisting of charges +3.2 x 10^-19 C and -3.2 x 10^-19 C separated by 2.0 x 10^-9 m is in a field of 5.0 x 10⁵ N/C. Calculate the torque on the dipole when the dipole moment is (a) parallel and in the same direction as the field (b) perpendicular to the field and (c) parallel and in the opposite direction of the field.

25.

There are really two types of problems concerning electric fields (a) given a distribution of charges, find the electric field due to them and (b) given an electric field E, find the electric force F_e on a charge q. Explain two ways of calculating electric fields and how you find the electric force on a charge q in an electric field.