1. Potential Energy Difference, U_B - U_A, between points A and B equals the work done W_AB carrying a positive test charge +q_o from A to B without increasing its kinetic energy.
   
   U_B – U_A = W_AB = _A∫^B F ^. ds, where F is the force you apply.
   
   For no change in kinetic energy, the magnitude of the object's velocity must remain constant so that there is no acceleration. For no acceleration, the net force acting on the object is zero.

   F_net = F + F_e = F + q_oE = 0  or
   F = - q_oE  and
   U_B - U_A = W_AB = - q_{o A}∫^B E ^. ds.

2. Potential Difference, V_B – V_A = V_BA = (U_B – U_A)/q_o = (-q_{o A}∫^B E ^.ds)/q_o

   V_B - V_A = - _A∫^B E ^. ds.

3. Potential Energy U at a point P equals the potential energy difference between point P and some point where the potential energy is taken to be zero.
   
   
4. Potential V at a point equals the potential energy U per unit charge.

   V = U/q_o.
   
   

1. Special Cases for Potential Energy Difference and Potential Difference
   
   
   1. Point charge q in field of a point charge +Q
      
      
      1. Potential Energy Difference U_B - U_A = kqQ(1/r_B – 1/r_A),
         where r_B is the distance of Q from point B
         and r_A is the distance of Q from point A.
         
         
      2. Potential Difference V_BA = (U_B - U_A)/q = kQ(1/r_B – 1/r_A)
         
         
   2. Point charge q in field of a parallel plate capacitor with +Q and - Q charge over area A and plate separation d.
      
      
      1. U_B - U_A = q(E)d = q(Q/A ε_o)d,
         where 1/4πε_o = k = 9.0 x 10⁹ N-m²/C².
         
         
      2. V_BA = (U_B - U_A)/q = Qd/A ε_o
         
         
2. Special Cases for Potential Energy and Potential
   
   
   1. In field of point charge take U at infinity equal to zero.  Then at point P a distance r from +Q the potential energy U = kqQ/r. If the charge is negative,  U = - kqQ/r.
      
      
      1. Since Potential V = U/q,  for +Q,  V = kQ/r and for - Q, V = - kQ/r.
         
         
      2. Since potential energy and potential are scalar quantities, we can use the negative sign to indicate a potential energy or potential less than zero. For example, if you move a +q away from the - Q that sets up the field without changing its kinetic energy, you do work. Thus the potential energy at infinity must be greater than at the point closer to the negative charge. This can only be true if the potential energy is negative near the negative charge - Q.
         
         
   2. If you have more than one charge setting up the field, you find the potential at a point due to each one and then add the potentials algebraically.
      
      
3. Sample problems in 106 Problem Set for Potential Energy, Potential, and Capacitors: 1-4.
   
   
   

U_B + K_B = U_A + K_A   or
U_B - U_A = K_A - K_B

1. Definition C = q/V_BA
   
   
   1. For a parallel plate capacitor, V_BA = qd/A ε_o and C = q/V_BA = A ε_o/d. Notice that C is a constant that depends only on the dimensions of the parallel plates and the constant ε_o.
      
      
   2. A charged sphere acts as though all the charge were at the center of the sphere.  At the surface of a sphere of radius R,
      V = kq/R  and C = q/V = R/k.
      
      
   3. When a dielectric of dielectric constant κ is inserted into a capacitor, its capacitance goes up by a factor of κ.
      
      
2. The potential energy stored by a capacitor U = 1/2 qV_BA = 1/2 C (V_BA) ² = 1/2 q²/C.
   
   
3. Note on units: 1 F = 1 C/V. For U = 1/2 C (V_BA) ², units of U are (C/V)(V)² = C - V = J. For U = 1/2 q²/C, units of U are C²/(C/V) = C-V = J. Sorry that coulomb C and capacitor C are confusing.
   
   
4. Capacitors in series and in parallel
   
   
   
   
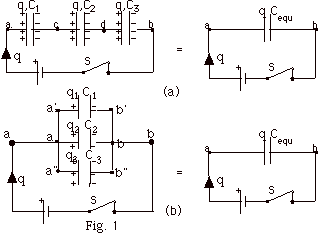
   1. For the three capacitors wired in series (Fig. 1a above),
      
      
      1. The charge q is the same on each.
         
         
      2. The potential difference across each is not the same unless the capacitance of each is the same. From conservation of energy,

         V_ab = V_ac + V_cd + V_db
         q/C_equ = q/C₁ + q/C₂ + q/C₃
         

         
         
      3. 1/C_equ = 1/C₁ + 1/C₂ +1/C₃, where C_equ is the equivalent capacitor which replaces the three individual capacitors and has the same charge q and the same potential difference V_ab. For capacitors in series, the reciprocal of the capacitances add to equal the reciprocal of the equivalent capacitance.
         
         
   2. For the three capacitors wired in parallel (Fig. 1b above),
      
      
      1. The potential difference across each is the same:

         V_a'b'= V_ab = V_a"b"
         

      2. From conservation of charge, q = q₁ + q₂ + q₃
         
         
      3. Since q = CV_ab,

         C_equV_ab = C₁V_ab + C₂V_ab + C₃V_ab  or
         C_equ = C₁ + C₂ + C₃.

         For capacitors in parallel, the sum of the individual capacitances equals the equivalent capacitance.
         
         
5. Sample problems in 106 Problem Set for Potential Energy, Potential, and Capacitors: 15, 17-20.