|
|
- Angle in radians
- An angle in radians is defined as the arc it subtends divided
by the radius of the circle. In Fig. 1 below, the angle
is Θ, the arc it subtends
is s, and the radius is R. Θ=
s/R. Notice that the unit of s is meters and the unit
of R is meters so the angle has no unit. We say radians
or degrees to distinguish which system we are using.
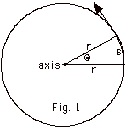
- Conversion of radians to degrees or degrees to radians
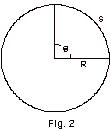
- The circumference of a circle equals 2 πR.
In Fig. 2 below,
s equals one-quarter of a circle, or s = 2 πR/4
= πR/2.
In radians Θ= s/R
= ( πR/2)/R = π/2.
In Fig. 2, Θ=
90o.
Thus π/2 radians =
90o, or π
radians = 180o.
- In general, (angle in radians)/(angle in degrees) =
π/180o.
- Descriptive Terms of Rotational Motion
- Speed v at any point = the magnitude of the velocity
tangent to the path at that point.
- For circular motion Period T = time for complete rotation
= 2 πr/v.
- The frequency f = reciprocal of period = 1/T = v/2 πr.
- The angular velocity ω
(omega not w) = the angle turned through per second or
for a varying angular velocity = dΘ/dt.
In Fig. 1, Θ= (1/R)(s)
(Equation
1)
Taking the derivative with respect to
t on both sides of Eq. 1,
dΘ/dt= (1/R)(ds/dt)
(Equation
2)
Recognizing dΘ/dt
as the angular velocity ω
and ds/dt as the linear velocity v gives us the relation
between ω and v.
ω = v/R. Since
the frequency f = v/2 πR
or v = 2 πRf, ω
= (2 πRf)/R = 2 πf=
2 π/T.
Unit of ω is s-1.
- Angular acceleration α
is the rate of change of angular velocity.
α= dω/dt.
Its unit is s-2.
For constant angular acceleration,

- ω2
= ωo2
+ 2α(Θ-
Θo)
Linear analogy, v2 = vo2
+ 2a(x – xo)
- Sample problems in 107
Problem Set for Angular Motion: 3-5.
- Rigid Body
- All points on the object rotate with the same angular
velocity ω.
- For every mass m1, m2 m3,
etc. that makes up the body,
v1 = ωr1,
v2 = ωr2,
v3 = ωr3,
etc. (See Fig. 3 below)
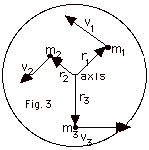
- K = 1/2 m1v12 + 1/2
m2v22 + 1/2 m3v32
+ + + +
= 1NΣ(1/2)
mivi2
K = 1/2 m1r12ω2
+ 1/2 m2r22ω2
+ 1/2 m3r32ω2
+ + +
= 1NΣ(1/2)
miri2ω2
Define Moment of inertia I = 1NΣ
miri2. Then K =
(1/2)Iω2
.
Compare with K = 1/2 mv2 for translation.
- If distribution of mass is continuous then integrate
to find moment of inertia
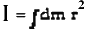
- Moments of Inertia
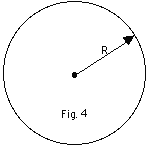
- Hoop (Fig. 4 below) All points on the hoop equal the distance
R from the axis of rotation. The moment of inertia of a hoop
about its center of mass = MR2.
- Circular Disk (Fig. 5 below). Now there is mass located
throughout the object.
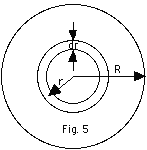
- The mass per unit area of the disk σ
= M/ π R2.
The area of a thin ring of radius r, thickness dr, dA
= 2πr dr. The mass
of a thin ring of radius r, thickness dr = dm = (mass
per unit area)dA = (M/ π
R2)(2πr
dr).
- The moment of inertia of a disk about its center of
mass is:
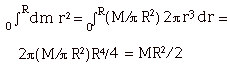
- A cylinder can be considered a series of disks. The moment
of inertia of a sphere about the center of mass I = 1/2 MR2.
- The moment of inertia of a sphere about its center of mass
I = 2/5 MR2.
(See Review 6, Problem 10)
- Thin Rod
- Mass/Length = M/L
- Mass of length dx = dm = (Mass/Length)dx = (M/L)dx
- dI = dm x2 = (M/L) x2 dx
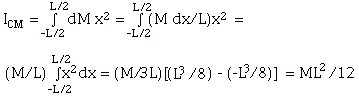
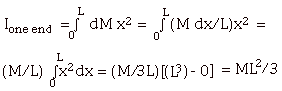
- About center of mass (Fig. 6a below),
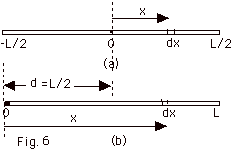
- About one end (Fig. 6b above),
- Parallel Axis theorem: I(parallel) = I(CM) + Md2,
where d is the distance between the axes
For rod about one end I = ML2/12 + M(L2/4)
= ML2/3
- Sample problems in 107
Problem Set for Angular Motion: 9-11.
- Application of Conservation of Energy to Rotation
- Object of mass M, radius R and moment of inertia ICM
is initially at rest at the top of an incline. The distance
between the center of the object at the top of the incline
and at the bottom of the incline is h (Fig. 7 below). It rolls
without slipping down the incline. A frictional force acts
on the object, but the frictional force acts at a point, not
through a distance so the frictional force does no work and
we can use conservation of energy to solve this problem.

- At the top,
Etop = U + K = Mgh + 0
- At the bottom since the sphere has both translational
and rotational kinetic energy,
Ebottom = U + K = 0 + (1/2 Mv2
+ 1/2 ICMω2)
- Since ω = v/R,
Ebottom = 1/2 Mv2 +
1/2 ICM(v2/R2)
- From conservation of energy,
Mgh = 1/2 Mv2 + 1/2 (ICM/R2)v2
or v2 = 2gh/(1 + ICM/MR2)
- Special Cases
- For hoop, ICM = MR2, v =
(gh)1/2
- For disk or cylinder, ICM = MR2/2,
v = (4gh/3)1/2
- For sphere, ICM = 2MR2/5,
v = (10gh/7)1/2
- Sample problems in 107
Problem Set for Angular Motion: 17, 18, 20-22,
25.
- Work Done on Rotating Rigid Body
- Since ω2
= ωo2
+ 2α(Θ - Θo),
1/2 ICM ω2
- 1/2 ICM ωo2
= ICMα(Θ - Θ)o).
- Identify the left-hand side of the above equation as ΔK
and the right hand side as the work W = ICMα(Θ - Θo).
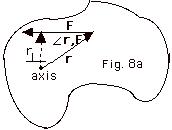
- Torque τ
- τ= r
x F
- Magnitude of τ = rF
sin
 r,F
= (r sin r,F
= (r sin  r,F)F = r,F)F =
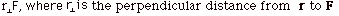
(See Fig. 8a below)
- Direction of torque. For τ= r x F, point the fingers of your
right hand in the direction of r with the palm of your
hand ready to rotate in to F. Rotate your fingers into
F. The thumb of your right hand points out of the page.
The torque τ is
out of the page. (See Figure 8b below)
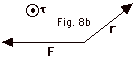
- Sample problems in 107
Problem Set for Angular Motion: 13-16, 19.
- Angular Momentum L
- For a point particle of mass m moving with velocity v,
L = r x mv,
where r is the distance from the axis to the position of the
mass m.
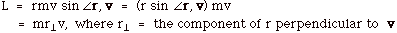
- For direction of L, point the fingers of your right
hand in the direction of r and rotate your fingers
into the direction of v, your thumb and the angular
momentum L point out of the page (Fig. 9 below)
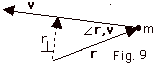
- For a rotating rigid body L = Iω.
The direction ofωis
found by curling the fingers of your right hand in the direction
of the rotation. Your thumb points to the direction of ω
and for a rotating rigid body to the direction of L.
- For point object,
dL/dt =
d(r x mv)/dt =
d(r)/dt x mv + r x d(mv)/dt =
[v x mv] + r x d(mv)/dt
=
0 + r x F,
because [v x v] = 0 and F = d(mv)/dt.
Thus dL/dt = r x F = τ
.
When the torque equals zero, the angular momentum remains
constant. When no external torque acts on a system, angular
momentum is conserved.
- For rotating rigid body,
- τ = dL/dt = d(Iω)/dt
= Iα
- Work = W = (Iα)Θ
= τΘ
- Conservation of Angular Momentum
- If no net external torque acts on a system, its total
angular momentum L remains constant. τ =
dL/dt. If τ
= 0, dL/dt = 0,
and L remains constant.
- Examples
- Person on rotating table
- Planetary motion
- Gyroscope
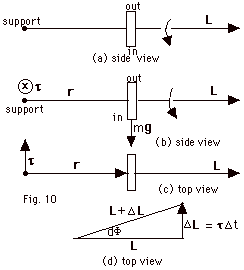
- Wheel spins clockwise as viewed from support
L is to the right. (Fig. 10a
above)
- The torque due to the weight mg is τ
= r x mg points into the paper.
(Fig. 10b above)
- As seen from above, L precesses slowly
counterclockwise. (Fig. 10 c and d above)
L + ΔL
= L + τ Δt,
where τ
= dL/dt.
d(L2)/dt = d(L .
L)/dt = L . dL/dt
+ L . dL/dt =
2L . dL/dt =
2L . τ
= 2Lτcos  L,
τ L,
τ
=2Lτcos 90o
= 0
Since τ
is perpendicular to L, there is no change
in the magnitude of L, only change is in its direction.
- dΦ = τdt/L
or
Ω = dΦ/dt
= τ/L = mgr/Iω.
Wheel spins at rate ω
and precesses at rate Ω.
- Sample problems in 107
Problem Set for Angular Motion: 26-37.
- Example
- Statement of the Problem
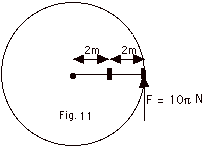
A piece of playground apparatus consists of two carts, each
of mass 50 kg, that are joined by very light (compared to
the mass of the carts) rigid rods, 2 m each in length,
as shown in Fig. 11 above. To make this device rotate, a child
applies a constant force of 10 πN
to the outer cart, directed perpendicular to the rods. The
apparatus is initially at rest.
Find:
- the moment of inertia of the apparatus,
- The angular acceleration produced by the child,
- how long it will take for the apparatus to make one
complete revolution,
- at the time for (3)
- the angular velocity, and
- the kinetic energy of the apparatus, and
- the work done by the child.
- Find the direction and magnitude of ΔL/ Δt
and the torque.
- Solution to the problem
- Treating the two carts as point particles,
I = 50 kg(2 m)2 + (50 kg)(4 m)2
= 1000 kg-m2.
- τ = r
x F
τ= (4 m)(10 πN)
sin 90o = 40 πN-m
= Iα = 1000 kg-m2α
α= 0.04 πs-1
- Angle turned through in one complete revolution = 2 π
= 1/2 αt2.
t = [(4 π)/α]1/2
= [(4 π)/4 πx
10-2 s-2]1/2 = 10 s
-
- (a) ω = ωo
+ at = 0 + (4 πx
10-2 s-2)(10 s) = 0.4 πs-1
- (b) K = 1/2 Iω2
= 1/2 (1000 kg-m2)(0.4 πs-1)2
= 80 π2
J
- W = τΘ= (40 πN-m)(
2 π) = 80 π2
J = Kf – KI = 80 π2
J – 0
- Since ωo
= 0, Lo = 0. Final L = Iω.
Since the apparatus rotates counterclockwise,
ω is
out of the page. After one revolution,
L = (1000 kg-m2)(0.4 πs-1)
= 4 πx102 m-kg/s.
ΔL/ Δt
= (4 πx102 m-kg/s)/(10
s) = 40 π m-kg/s2
= τ out of page.
- Combination of Translational and Rotational Motion
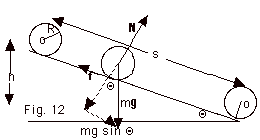
- For a sphere to roll without slipping down the incline
plane there must be a frictional force f.
- We need two equations of motion, one for translation and
one for rotation.
- For translation,
Fnet = ma
mg sin Θ - f = ma
(Equation
1)
- For rotation about the center of mass, neither N
nor mg produces a torque about the center of mass
because their line of actions pass through the center
of mass.
τCM
= ICMα
fR sin 900 = (2/5 mR2)α
or
since
α = a/R,
f = 2/5 ma
(Equation
2)
Substituting (2) into (1):
mg sin Θ - 2/5 ma
= ma or
a = 5g sinΘ/7 v2
= v02 + 2as = 0 + (10/7)g(s sinΘ)
= (10/7)gh,
v = (10gh/h)1/2, as we found before using conservation
of energy.
- Conditions for Equilibrium
- The sum of the external forces must be zero, or
Σ F
= 0
- The sum of the external torques must be zero, or
Στ
= 0
- Example (Fig. 13a below):
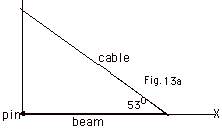
A uniform horizontal beam of length 8.00 m and weight 200
N is attached to a wall by a pin connection. A cable that
makes an angle of 53.0o with the horizontal (Fig.
13a above) supports its far end. If a 600-N person stands
2.00 m from the wall, find the tension in the cable and
the force exerted by the wall on the beam.
- Solution to Example (Fig. 13b below):
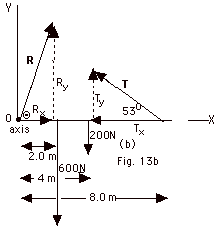
- The forces acting on the beam are:
- The gravitational force of the earth on the beam,
its weight = 200 N acts at the center of the uniform
beam.
- The force of the man on the beam = 600 N
- The tension T in the rope
- The force R exerted by the wall at the pivot
- The torques acting on the beam about the axis at the
pivot point are:
- Torque due to R is zero because it acts at the
pivot point. Any force that passes through the axis
produces no torque (r = 0).
Note:
I chose the axis at the pivot point to eliminate one
of the unknowns in the torque equation, leaving only
T as an unknown.
- The torque due to the tension in the rope = 8.0
m(T) sin 53o
out of the page.
- The torque due to the force of the man = 2.0 m(600
N)
into the page
- Since it is a uniform beam, the weight of the beam
acts at the center.
r = 4 m for the beam weight.
Torque = 4.0 m(200 N) into the page.
- Στ
= 0
Taking out of the page as positive:
+8.0 m(T) sin 53o - 2.0 m(600
N) - 4.0 m(200 N) = 0
8.0 m(T)(0.80) = 2000 N-m. T
= 313 N
- The vector sum of the forces must = 0.
Change this two-dimensional problem into two one-dimensional
problems, by taking the components of the tension T
and the force of the wall at the pivot R into X
and Y components.
As shown in Fig. 12b,
Tx = T cos 53o
Ty = T sin 53o,
Rx = R cos Θ,
and
Ry = R sin Θ
| ΣFx = 0 |
ΣFy = 0 |
| R cos Θ
- T cos 53o = 0 |
R sin Θ
+ T sin 53o – 600N – 200N
= 0 |
| R cos Θ
= T cos 53o |
R sin Θ
= - T sin 53o + 600 N + 200 N |
| R cos Θ
= 313(0.6) |
R sin Θ=
-313 N(0.8) + 800 N |
| R cos Θ
= 188 N (Equation
1) |
R sin Θ=
550 N (Equation
2) |
Dividing Eq.2 by Eq. 1:
tan Θ=
550 N/188 N = 2.92. Θ
= 71.10 R.
R sin Θ= 550 N.
R = 550 N/sin Θ.
R = 550 N/sin 71.1o = 581 N.
- Sample Problems in 107
Problem Set for Angular Motion: 22-24.
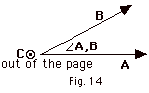
- Using Cross Product with Unit Vectors
- Definitions
- Magnitude of C = A
x B is C = |A||B|cos
 A,
B. A,
B.
- Point the fingers of your
right hand in the direction of A with your palm
toward B. Rotate your palm into B.
Your thumb points in the direction of C. In
Fig. 14 below, C is out of the page.
- Application to unit vectors
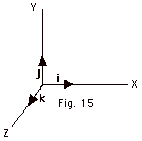
- i x i = |i||i|sin
 i,
i = |1||1|sin 0o
= 0 i,
i = |1||1|sin 0o
= 0
j x j = |j||j|sin  j,
j = |1||1|sin 0o
= 0 j,
j = |1||1|sin 0o
= 0
k x k = |k||k|sin  k,
k = |1|1|sin 0o = 0 k,
k = |1|1|sin 0o = 0
- Magnitudes and Directions
- Magnitude: |i
x j| = |i||j|sin
 i,
j = |1||1|sin 90o
= 1 = |j x i| i,
j = |1||1|sin 90o
= 1 = |j x i|
Direction: i x j = k
j x i = - k
- Magnitude: |i
x k| = |i||k|sin
 i,
k = |1||1|sin 90o
= 1 = |k x i| i,
k = |1||1|sin 90o
= 1 = |k x i|
Direction: i x k =- j k
x i =j
- Magnitude: |j
x k| = |j||k|sin
 j,
k = |1||1|sin 90o
= 1 = |k • j| Direction: j
x k = i k x
j = - I j,
k = |1||1|sin 90o
= 1 = |k • j| Direction: j
x k = i k x
j = - I
- Sample Problem in 107
Problem Set for Angular Motion: 12.
|
|