Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 107

Outline - Center of Mass, Momentum, and Collisions
  1. Center of Mass

    1. The center of mass of an extended system is the point whose dynamics typifies the system as a whole when it is treated as a particle.

    2. Sample Problem. Find the location of the center of mass of the system of three particles shown in Fig. 1 below. Each particle has the same mass m. The coordinates (x,y,z) of particle 1 are (0,L,0) of particle 2 are (0,0,0) and of particle 3 (L,0,0).

    3. XCM = (1/3m)[0(m) + 0(m) + L(m)] = L/3
      YCM = (1/3m)[L(m) + 0(m) + 0(m)] = L/3
      ZCM = (1/3m)[0(m) + 0(m) + 0(m)] = 0

    4. Symmetry arguments show that the center of mass of a uniform rectangular plate, a uniform spherical shell, a uniform sphere or a sphere with a spherically symmetric distribution of mass is located at the geometric center of the object.

    5. Two Methods to find center of mass



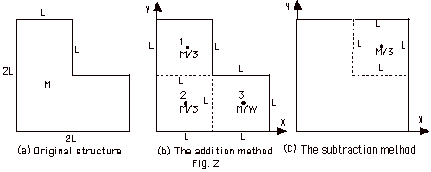
      Addition method: In Fig. 2(a) above, I show a thin sheet of metal in the shape of an L.  In Fig. 2(b) above, I have indicated the center of mass of each segment. For segment 1, the (x,y) coordinates are (L/2, 3L/2), for segment 2 they are (L/2, L/2), and for segment 3 are (3L/2, L/2). Note that we do not need a Z-component for the thin sheet.

      Since each segment has mass M/3,
      XCM = (1/M)[L/2(M/3) + L/2(M/3) + 3L/2(M/3)] = 5L/6
      YCM = (1/M)[3L/2(M/3) + L/2(M/3) + L/2(M/3)] = 5L/6

      Subtraction Method: In Fig. 2(c) above, the center of mass of the square is at the center of the square. The X-Y coordinates are (L, L). The center of mass of dashed square is (3L/2, 3L/2). The X-component center of mass of the original figure in 2a is the X-component of the center of mass of the square minus the X-component of the "added" square. A similar approach finds the Y-component of the original figure.
      XCM = (1/M)[L(4M/3) - 3L/2(M/3)] = 5L/6
      YCM = (1/M)[L(4M/3) - 3L/2(M/3)] = 5L/6

    6. Center of Mass for Continuous Medium

      1. Densities:

        1. Linear density λ= mass/length or mass = λ(length)

        2. Surface density σ= mass/area or mass = σ(area)

        3. Volume density ρ= mass/volume or mass = ρ(volume)

      2. The equations become:


      3. Applications:

        Find the centers of mass of the three objects below:



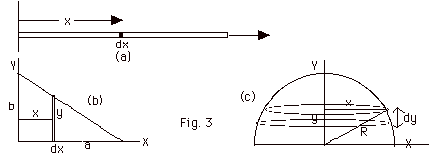
        (a) Were the "line" of mass uniform, the problem would be trivial. The center of mass would be at the center of the rod. To make the problem more interesting let λ = λo(x/L), where λo = a constant and L = the length of the rod. For the element of length dx, its mass element of mass dm = λ dx = λo(x/L) dx.





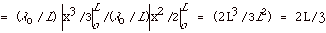
        (b) Mass/area = σ.     σ(area) = mass.

        For mass of area dA =ydx (see Fig.3b above), dm = σdA = σydx.
        The area of the triangle = ab/2.  Let the mass of the triangle = M,
        then σ = Mass/area = M/(ab/2) = 2M/ab.


               
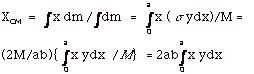
        The last equation involves two variables. You must eliminate one of them. The equation of the line
        y = (slope)x + intercept on Y-axis
        y = - (b/a)x + b



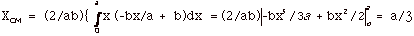
      (c) The volume of a hemisphere is 2 πR3/3.
           The density of the hemisphere ρ =

      Mass/volume = M/(2 πR3/3) = 3M/2 πR3.
      In Fig. 3(c) above, the volume of an element dV = πx2 dy.
      The mass of the element dm =
      ρdV = (3M/2 πR3) πx2 dy.
      Notice that x2 = R2 - y2 and that dm = (3M/2 πR3) π(R2 - y2) dy.




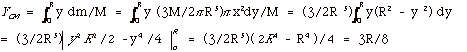
    7. Sample problems in 107 Problem Set for Momentum: 2, 4, 8, 9.



  2. Linear Momentum p

    1. Linear momentum of an object p = mv, where v is the velocity of an object of mass m. Linear momentum is a vector quantity. p has the same direction as the velocity v.

    2. Newton's second law Fnet external = ma can be rewritten in terms of momentum. Since a = dv/dt, we can rewrite ma = d(mv)/dt. If m is a constant, then you can take it outside of the derivative and m dv/dt goes back to ma. Newton actually wrote the second law as Fnet external = dp/dt.

    3. If no net external forces act on a system dp/dt = 0 and the momentum of the system remains a constant. Linear momentum is conserved.

    4. In "collision problems," momentum is always conserved, but energy is only conserved for elastic collisions. In Fig. 4 below, an object of mass m1 = 2 kg moves to the right with a speed of v1i = 5 m/s. It collides with a mass mass m2 = 3 kg initially at rest. After the collision, the two objects stick together and move with a velocity vf.



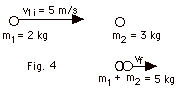
      We find the velocity after the collision using conservation of momentum. The initial momentum of the system equals the final momentum:

      pI = pf
      2kg(5 m/s) = (2 + 3)kg vf, or vf = 2 m/s

      The initial kinetic energy of the system = 1/2 (2 kg)(5 m/s)2 = 25 J
      The final kinetic energy of the system = 1/2 (5 kg)(2 m/s)2 = 10 J

      While momentum is always conserved in a system, kinetic energy is only conserved in an elastic collision. This is an inelastic collision.

    5. Since momentum is a vector quantity, you may consider the conservation of the components of momentum. If two vectors are equal, their components are equal. If the initial momentum
      pi = pf
      the final momentum then,
      (pi)x = (pf)x and     (pi)y = (pf)y
      An object of mass 4m is initially at rest. It breaks into three parts, two of mass m and one of mass 2m. After the explosion, one of the objects of mass m moves along the negative Y-axis with a speed of 10 m/s and the other one of mass m moves along the positive X-axes (Fig. 5a below).



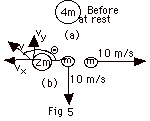
      Find the magnitude and the direction of the velocity of 2m after the explosion. The initial momentum of the system is zero. After the collision one of the pieces moves in the +X direction and the other moves in the -Y direction (Fig. 5b above).

      To solve this problem you must separate it into two one-dimensional problems:

      (pi)x = (pf)x
      0 = m(10 m/s) + 2mvx
      vx = - 5 m/s  (the minus sign indicates that it is to the left)

      (pi)y = (pf)y
      0 = m(-10 m/s) + 2mvy
      vy = +5 m/s  (the plus sign indicates that it is up)

      v = (vx2 + vy2)1/2 = (25 + 25)1/2 m/s = 5√2 m/s
      Tangent of the angle that v makes with X axis = vy/vx = 5/-5 = -1
      Angle Θwith the +X-axis = 135o

    6. Kinetic energy is conserved in an elastic collision



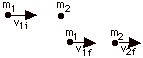
      For the elastic collision shown in the figure above

      pi = pf
      m1v1i = m1v1f + m2v2f       (Equation 1)
      Ki = Kf
      1/2 m1v21i = 1/2 m1v21f + 1/2 m2v22f      (Equation 2)


      Solving Eq. 1 and Eq. 2 for v1f and vf2:
      (if they are not in the direction shown in the figure, your calculation will give you a minus sign)

      v1f = [(m1 - m2)/(m1 + m2)]v1i
      v2f = [(2m1)/(m1 + m2)]v1i

      Special cases
      1. If m1 = m2,  v1f = 0 and v2f = v1i
        All momentum and energy of m1 transferred to m2

      2. If m2 >> m1,  v1f » -v1i and v2f ≈ (2m1/m2)v1i

        Momentum transferred to m2 = m2v2f = 2m1v1i = 2p1 for greatest amount of momentum transferred

        Kinetic energy transferred to m2 = (2m21/m2)v21f, a very small amount, because m1 << m2
                         
      3. If m1 >> m2,  v1f » vii


    7. Sample problems in 107 Problem Set for Momentum: 5-7.


  3. Impulse J
    1. Impulse J = d(mv) =dp = Favdt, where Fav is the average force.

    2. Impulse-momentum theorem states that the impulse equals the change in linear momentum. J = mvf - mvi. Since impulse and momentum are vector quantities, you may set the X-component of the impulse equal to the change in the X-component of momentum and the Y-component of the impulse equal to the change in the Y-component of momentum.

    3. Sample problems in 107 Problem Set for Momentum: 1, 3, 10-25.

Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
October 8, 2002
April 17, 2003