Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 107

Outline - Newton's Laws
  1. Newton's Laws

    1. First Law. An object at rest remains at rest and an object moving with velocity v remains moving with velocity v if and only if no net external force acts on the object.

    2. Second Law. The net force acting on an object is directly proportional to and in the same direction as the acceleration. The proportionality constant is the mass of the object.
                   Fnet = ma

    3. Third Law. When two objects interact in whatever manner, the force
      F12  exerted by the first object on the second is equal in magnitude and opposite in direction to the force F21 of the second object on the first.
      -F12 = F21


  2. Application of Newton's Laws



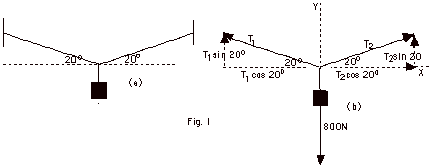
    1. An object hanging motionlessly in Fig. 1 above has a weight of 800 N. Find the tensions T1 and T2 in the massless ropes. For the object to be at rest, the sum of the forces acting on the object must be zero. Since the tensions are neither in the X nor Y-direction, take components:

      (Fnet)x = max = 0

      (Fnet)y = may = 0

      T2 cos 20o – T1 cos 20o = 0

      T2 sin20o + T1 sin20o – 800N = 0

      T2 cos 20o = T1 cos 20o

      T2 sin20o + T1 sin20o = 800N

      T2 = T1 = T       2T sin20o = 800 N       T = 1.17 x 103       N = T2 = T1

    2. When you apply Newton's second law, you must be very careful about your choice of system.



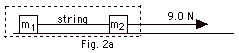
      1. Imagine two masses m1 = 1.0 kg and m2 = 2.0 kg are connected by a massless string and are pulled along a frictionless surface by a force F = 9.0 N as shown in Fig. 2a above. Find (a) the acceleration of the blocks and (b) the tension in the string.

        1. In Fig. 2a, I have isolated the entire system of the two blocks. There are vertical forces acting on both blocks: the normal force of the surface and the weight of each block. Since there is no acceleration in the vertical direction and there is no friction (we would need to know the normal force in order to find the frictional force on a block), we shall not consider forces in the vertical direction. The only external horizontal force acting on the system is F = 9.0 N. There are internal horizontal forces acting on the blocks and the string, but we are not interested in internal forces because
          Fnet external = msystem a
          9.0 N = [(1.0 + 2.0)kg] a
          and a = 3.0 m/s2



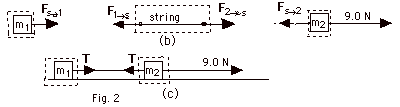
        2. Now we choose our system as shown in Fig. 2b and 2c above. Again I only look at the horizontal forces. I have isolated:

          1. the string experiencing F1s, the force of block 1 on the string and F2s, the force of block 2 on the string

          2. m1 experiencing Fs1 = the force of the string on
            block 1

          3. m2 experiencing Fs2, the force of the string on block 2 and F = 9.0 N.

        3. For the string, Fnet external = mstringa
          F2s -  F1s = (0)3.0 m/s2 = 0
          So   F2s = F1s
          By Newton's Third Law,  Fs2 = F2s  and  Fs1 = F1s
          Thus,  Fs2 = F2s = F1s = Fs1.
          We drop all this fancy notation and write
          Fs2 = F2s = F1s= Fs1 = T,  as shown in Fig. 2c above.

        4. For m1, Fnet external = m1a
          T = 1.0 kg(3.0 m/s2) = 3.0 N

          For m2, Fnet external = m2a
          9.0 N – T = 2.0 kg(3.0 m/s2) = 6.0 N
          T = 3.0 N

    3. As you can see from the above example, Newton Third Law of Motion forces always act on different objects. In other words, they do NOT act on the same object.

    4. Sample problems in 107 Problem Set for Newton's Laws: 1-6.



  3. Frictional Forces

    1. The frictional force f = µN, where the coefficient of friction µ is labeled with a subscript s for static situations and k for objects in motion. The coefficient of friction for static situations is always greater than that for kinetic. The static frictional force can go from 0 to a value necessary to just about move the object.



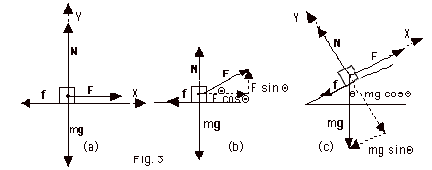
    2. Finding the frictional force (Fnet)y = may = m(0) = 0

      1. For Fig. 3a above, N - mg = 0.
        N = mg and f = µN = µmg

      2. For Fig. 3b, N + F sin Θ - mg = 0.
        N = mg - F sin Θ and f = µN = µmg - F sin Θ)

      3. For Fig. 3c, N - mg cos Θ= 0.
        N = mg cos Θ; f = µN = µmg cos Θ

    3. Sample problems in 107 Problem Set for Newton's Laws: 7-11.


  4. Gravitational force Fg = Gm1m2/r2, where m1 and m2 are the masses of two point particles separated by a distance r.

    1. Near the earth's surface at height h very small compared to the radius of the earth RE. You can treat a spherical mass ME as a point mass located at the center of the earth. The force on an object of mass m at height h above the earth by the earth is Fg = GmME/(RE + h)2. Since RE is much greater than h, drop the h and Fg = GmME/RE2.

                  In general,                     Fnet = ma

    2. For a freely falling object, GmME/RE2 = ma
      For free fall a = g             GmME/RE2 = mg = Weight of object

    3. (mg) is not a mass times an acceleration, it is a force. To determine the direction of the force in a problem, decide on a direction to call positive and then see if mg is in that direction.  After doing this, never substitute
      -9.8 m/s2 for g in (mg).

      Example: An astronaut puts a bowling ball into a circular orbit about the Earth at an altitude h of 350 km. Find the ball's period of motion. The radius and mass of the earth are M = 5.98 x 1024 kg and
      R = 6.37 x 106 m, respectively.

      Answer to Example: The radius of the orbit of the bowling ball r = the radius R of the earth + the height h above the earth's surface =
      (6.37 + 0.35)106 m, and the constant in Newton's law of gravitation G = 6.67 x 10-11 N-m2/kg2. The gravitational force produces the centripetal acceleration:

         

      Fnet = ma
         

      GMm/r2 = mv2/r              (Equation 1)
       

      Since v = 2πr/T,

      GMm/r2 = m(2πr/T)2/r
        or

      T2 = 4π2 r3/GM        and
       

      T = 2 π (r3/GM)1/2

      		  
       

         = 2{(6.72 x 106 m)3/6.67 x 10-11 N-m2/kg2 x 5.98 x 1024 kg}1/2
       

         = 55 x 102 s

      		  

                                  


  5. Free Body Diagrams

    1. Force Diagrams such as those shown in Fig. 4 below are called Free-body diagrams. They are extremely important in solving Newton Second Law of Motion problems.



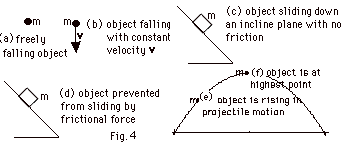
    2. In each situation shown in Fig. 4 above, one or more forces act upon an object. All drawings are in a vertical plane and friction is negligible except in (b) and (d). Draw free body diagrams for the figures, scale the forces as close as possible. Label all the forces acting on the objects. If the object has an acceleration, show its direction. If there is no acceleration, indicate that it is zero.



    3. In Fig. 4' above, (a) the only force that acts on the object is its weight mg. Its acceleration a is down. (b) For a constant velocity, the net force acting on the object must be zero. The upward frictional force equals the weight of the object. (c) There is no net force perpendicular to the plane. The normal force is equal to the component of the weight perpendicular to the plane. The component of the weight parallel to the plane gives the acceleration down the incline. (d) Now in addition to the forces talked about in (c) there is a frictional force up the plane that is equal in magnitude to the component of the weight parallel and down the plane. There is no acceleration. (e) and (f) The only force acting on an object in projectile motion (neglecting a frictional force) is the weight of the object down. The acceleration is down.

    4. Separating Objects in Free Body Problems

      Example:



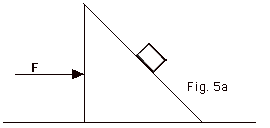
      A rectangular block of mass m1 rests on an inclined plane of mass m2, as illustrated in Fig. 5a above. There is neither friction between the block and the incline nor between the incline and the surface on which it moves. Find an expression for F in terms of m1, m2, and angle of the incline Θ so that the block remains at rest with respect to the incline.

      Solution:



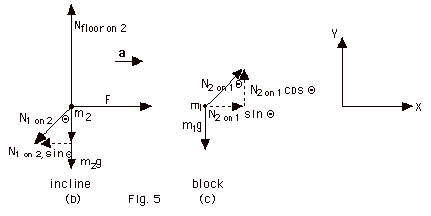
      In Fig. 5b above the forces acting on the incline of mass m2 are the normal force of the block on the incline N1 on 2,  the normal force of the floor on the wedge Nfloor on wedge,  the attraction of the earth for the incline, its weight, m2g, and the applied force F.

      In Fig. 5c above, the forces acting on the block of mass m1 are the normal force of the incline on the block N2 on 1 and the attraction of the earth for the block, its weight, m1g.

      Using the principle of superposition we divide the problem into the forces in the X and Y direction.

      For m1,

      X Y
                  (Fnet)x = m1a
      N2 on 1 sin Θ1 = m1a
                                       (Equation 1)       		                  (Fnet)y = m1(0) = 0
      N2 on1 cos Θ- m1g = 0
      N 2 on1 cos Θ= m1g
                                              (Equation 3)


      For m2,

      X Y
                       (Fnet)x = m2a
      F - N1 on 2 sin Θ1 = m2a
                                        (Equation 2)       		                          (Fnet)y = m1(0) = 0
      Nfloor on 2 - N1 on 2 cos Θ- m2g = 0


      By Newton's third law of motion,
      N2 on 1 = N1 on 2
      We may rewrite Eq. (2) as:
      F - N2 on 1 sin Θ1 = m2a           (Equation 2')
      Substitute Eq. (1) into Eq. (2'):
      F - m1a = m2a or F = (m1 + m2)a              (Equation 4)
      Divide Eq. (1) by Eq. (3):


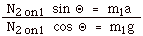
      or  tan Θ= a/g and a = g tan Θ           (Equation 5)
      Substitute Eq (5) into Eq. (4):
      F = (m1 + m2) g tan Θ
    5. Sample problems in 107 Problem Set for Newton's Laws: 12-24.

Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
October 8, 2002
April 16, 2003