Click here to return to Phyllis Fleming's homepage Phyllis Fleming Physics

Physics 108

Outline - Potential Energy, Potential, and Capacitors
  1. Energy

    1. Potential Energy Difference, UA - UB, between points B and A equals the work done WBA  by you in carrying a positive test charge q' from B to A without increasing its kinetic energy.

      UA - UB = WBA =

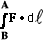
      For no change in kinetic energy, the magnitude of the object's velocity must remain constant so that there is no acceleration. For no acceleration, the net force acting on the object is zero. The vector sum of your force F and the force Fe exerted by the electric field must be zero.

      Fnet = F + Fe = F + q'E = 0  or  F = - q'E   and
      UA - UB = WBA =

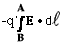
    2. Potential Difference VA - VB = VAB equals the potential energy difference divided by q',  or :
      VA - VB = VAB = (UA - UB)/q' =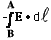

    3. Potential Energy U at a point P equals the potential energy difference between that point P and some point where the potential energy is taken to be zero.

    4. Potential V at a point P equals the potential energy at point P divided by q',  or :

      V = U/q'

    5. Finding electric field from the potential function

      Since V = - ∫ E dr,  -dV/dr = E.

      If you know V, you can find the components of the electric field from the negative partial derivative of V for that component (x, y, z, r, Θ, and so forth).


  2. Finding potential energy and potential functions from
           
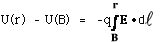
    1. For point charge, E = kQ/r2.  Take U(B) = 0 when rB = ∞.



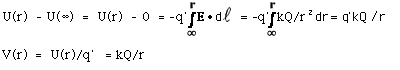
      Note: U is the potential energy of a system that consists of two or more charges. V is the potential at a point P due to a single or more charges.

    2. You find the potential due to a group of point charges by finding the potential due to each one, assigning a plus sign for a positive charge and a negative sign for a negative charge. Since potential and potential energy are scalar quantities, the resultant potential or potential energy is the algebraic sum of the individual potentials or potential energies. In Fig. 1 below, VP = kq1/r1 - kq2/r2.



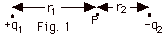
    3. For an extended distribution of charge, take an element of charge dq.
      dV = kdq/r.  Integrate to find V for a given situation.



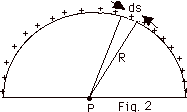
      1. As an example of an extended distribution take the case of positive charge spread uniformly along a semicircle (Fig. 2 above). You wish to find the potential at the center, point P, of the circle of radius R.  For the element of length ds with charge dq,
        dV = kdq/r = kdq/R.
          V = k/R ∫ dq = kQ/R,
        where Q is the total charge on the semi-circle.



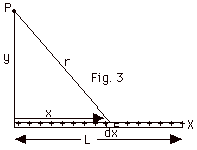
      2. A more complicated problem is shown in Fig. 3 above because the distance r from the element of charge is a variable. The element of charge dq on the element of length dx is the charge per unit length times dx, or dq = λ dx.  For any element dV = k dq/r = k λ dx/r.

        The problem here is you have two variables, r and x, and you must put one in terms of the other, plus a constant.  But r = (x2 + y2)1/2,
        where y, the Y-coordinate of P, is a constant.

        Then dV = k λ dx/r = k λ dx/(x2 + y2)1/2
                  

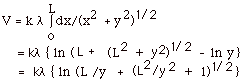
  3. Calculation of potential difference for distribution of charges

    1. Parallel plate capacitor (Fig. 4)



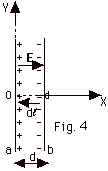
      This capacitor is used so frequently that it is worth considering again. For one "infinite" plane E = σ/2 εo, where σ = q/A.  For the parallel plate capacitor, both plates produce an electric field to the right (the direction in which a positive test charge is urged) and the electric field between the plates E = σ/ εo.  The potential difference between the plates,



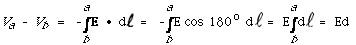
      since E = σ/ εo,  Va - Vb = σd/ εo


    2. Concentric sphere and shell (Fig. 5)




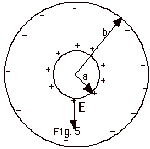
      If the sphere of radius a is a conductor, the electric field for r < a is zero. Whether it is a conductor or not, the electric field for a > r < b is due only to the charge enclosed by a Gaussian surface with a < r < b.  Also the sphere of radius a acts like a point charge Q at the center of the sphere and the electric field E = kQ/r2.

       



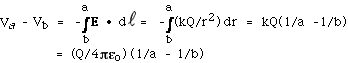
    3. Coaxial cylinders (Fig. 6)

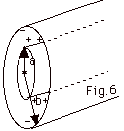      The electric field between the cylinder of radius a and the cylindrical shell of radius b is due only to the charge on the inner cylinder, as illustrated in Fig. 6.

      For  a < r < b,  E = λ/2πεo





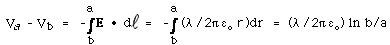
  4. Capacitance

    1. Definition C = q/Vab.
      C is a constant that depends only on the geometry of the capacitor.

      1. For parallel plate capacitor,
        C = q/Vab = q/(σd/ εo) = σA/(σd/ εo) = εoA/d
        = a constant depending only on geometry of capacitor.

      2. For sphere and concentric spherical shell,
        C = q/Vab = q/[q(b - a)/4πεoab] = 4πεoab/(b - a).
        C is a constant that depends only on the geometry of the capacitor.

      3. For coaxial cylinders,
        C = q/Vab = q/[(q/L2πεo)ln b/a] = 2Lπεo/ln b/a
        = a constant that depends only on the geometry of the capacitor.


    2. Capacitors in series and in parallel



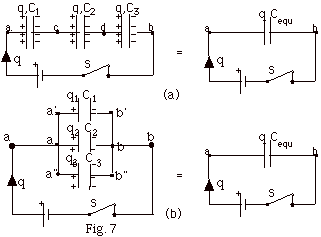
      1. For the three capacitors wired in series (Fig. 7a above),

        1. The charge q is the same on each.

        2. The potential difference across each is not the same unless the capacitance of each is the same. From conservation of energy,
          Vab = Vac + Vcd + Vdb
        3. Since Cequ = Vab/q,
          Vab/q = Vac/q + Vcd/q + Vdb/q

        4. 1/Cequ = 1/C1 + 1/C2 +1/C3,  where Cequ is the equivalent capacitor which replaces the three individual capacitors and has the same charge q and the same potential difference Vab. For capacitors in series, the reciprocal of the capacitances add to equal the reciprocal of the equivalent capacitance.

      2. For the three capacitors wired in parallel (Fig. 7b above),

        1. The potential difference across each is the same:
          Va’b’= Vab = Va”b”
        2. From conservation of charge,  q = q1 + q2 + q3

        3. Since q = CequVab,
          CequVab = C1Vab + C2Vab + C3Vab   or
          Cequ = C1 + C2 + C3
          For capacitors in parallel, the sum of the individual capacitances equals the equivalent capacitance.

    3. Energy associated with capacitors

      U = 1/2 qVab
      Since  C = q/Vab,  U = 1/2 q2/C = 1/2 CVab2

    4. The unit of capacitance is the farad (F). Since C = q/Vab, 1 F = 1 C/1 V.


  5. Using the parallel plate capacitor, you find the electrical energy per unit volume stored in an electric field is uE = 1/2 εo E2.  The electrical energy stored in volume dV is dUE = 1/2 εo E2 dV, where dV = 4 πr2 dr for a spherical shell and dV = 2 πrL dr for a cylindrical shell of length L.

  6. Dielectrics

    All the expressions for electric forces, fields, potential energies, potential, and capacitance are changed when a dielectric is present. The symbol ε0 is replaced by κε0, where κ is the dielectric constant. A dielectric in a medium produces an induced field that opposes the field set up by the initial charge distribution. The electric field is decreased, but the capacitance of a capacitor is increased since κ is always greater than zero.

  7. Sample Problems in 108 Problem Set for Potential Energy, Potential, and Capacitors:  1 - 6,  8 - 11, 13, 15, 16-19, 22-27.

Homepage Sitemap
     

Website Designed By:
Questions, Comments To:
Date Created:
Date Last Updated:

  

Susan D. Kunk
Phyllis J. Fleming
August 8, 2002
April 29, 2003